[ベスト] 対称な図形 問題 188908-対称な図形 点対称 問���

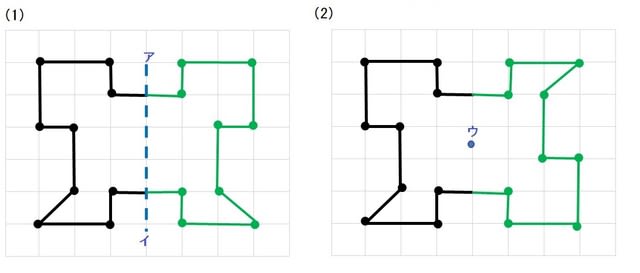
何かと教えづらい 線対称 点対称 小６ 算数の教え方教えますmother S Math Happy Study Support

小学校受験ではペーパーでも個別検査でも図形の問題がよく出題されます。 例えば、パズル、回転図形、線対称図形など。 今回は、息子が年中の12月に受けた模試のなかの対称図形の問題を一部変えて紹介します。 目次 対称図形の問題 年中12月の対称 中学1年数学 対称な図形 練習問題1 解答・解説 図の直線ℓが対称の軸になるように、線対称な図形を完成してください。 線対称な図形は、ℓで折った時に、ぴったりと重なり合うという性質が ありますから、左側の図形と

対称な図形 点対称 問題

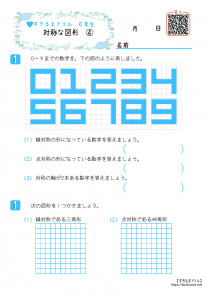
対称な図形 点対称 問題-③ 対称の軸が1本となる図形をすべて選びましょう 2 下の二つの図は点対称な図形です。対称の中心を見つけて、図の中に書きましょう。 6年 なまえ ひにち 月 日 りかい度 むずかしかった 〇 ふつう チェック りかいできた 対称な図形（問題1）ある直線を折り目として折り返したとき，両側の図形がピッタリと重なる図形を 線対称 な図形といい，このときの直線を 対称の軸 といいます。 「小学校で線対称な図形を学ぶ」など「線対称」という用語が使われている教科書は，T社，K社など

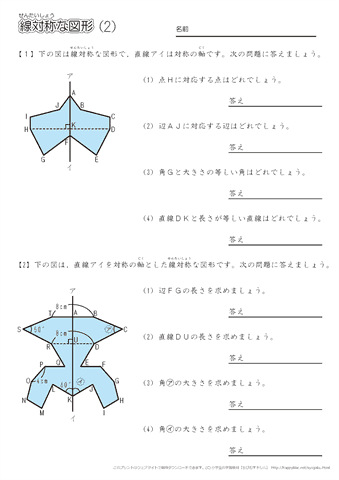
小学６年生の算数 線対称な図形 問題プリント ちびむすドリル 小学生

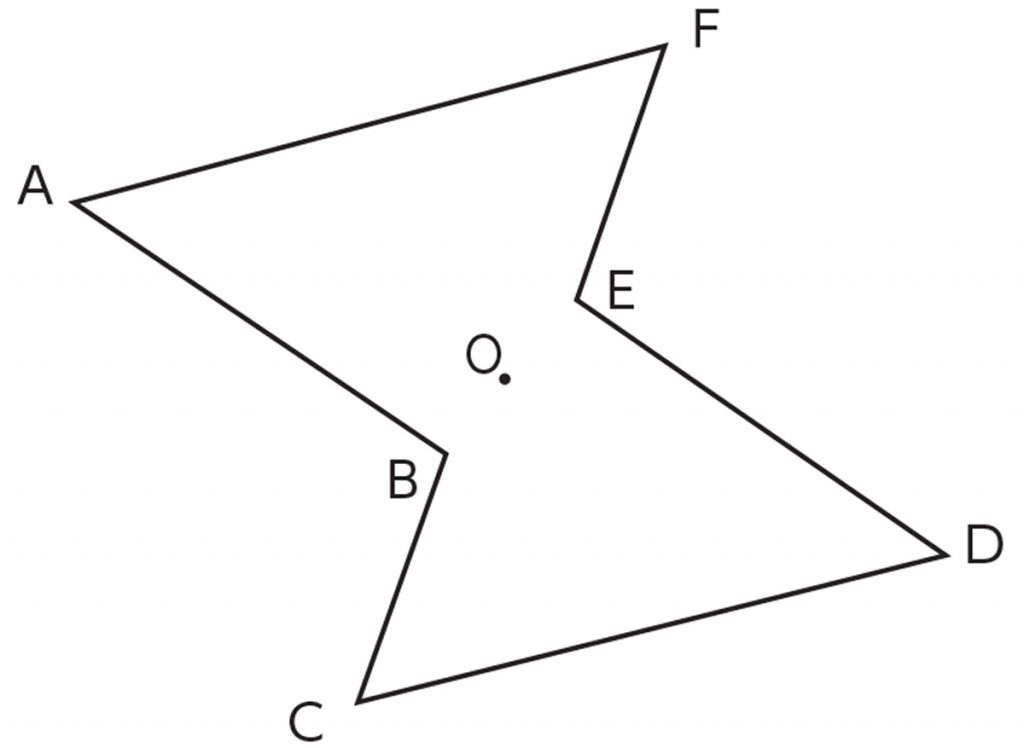
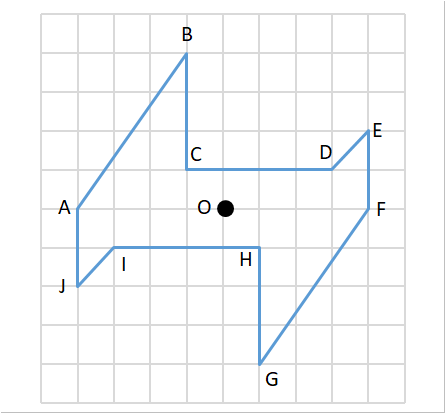
平面図形 問題 z 線対称な図形 z点対称な図形 z 平面図形の用語 z 作図 垂線 垂直二等分線 角の二等分線 z 作 図の応用 ＊「ページ表示」を「見開き」でご覧いただきますと、問題とその 答えが見やす== 点対称な図形 == 解説 次の図のように，ある点を中心に180°回転させたとき，元の図形と一致する図形を点対称な図形といいます。 このとき回転の中心となる点を対称の中心といいます。 右の図は平行四辺形が対角線の交点を対称の中心とする点対称な図形であることを示しています。 中学1年数学 対称な図形 練習問題4 解答・解説 図の六角形ABCDEFは点対称な図形で、点Oは対称の中心です。 次のに

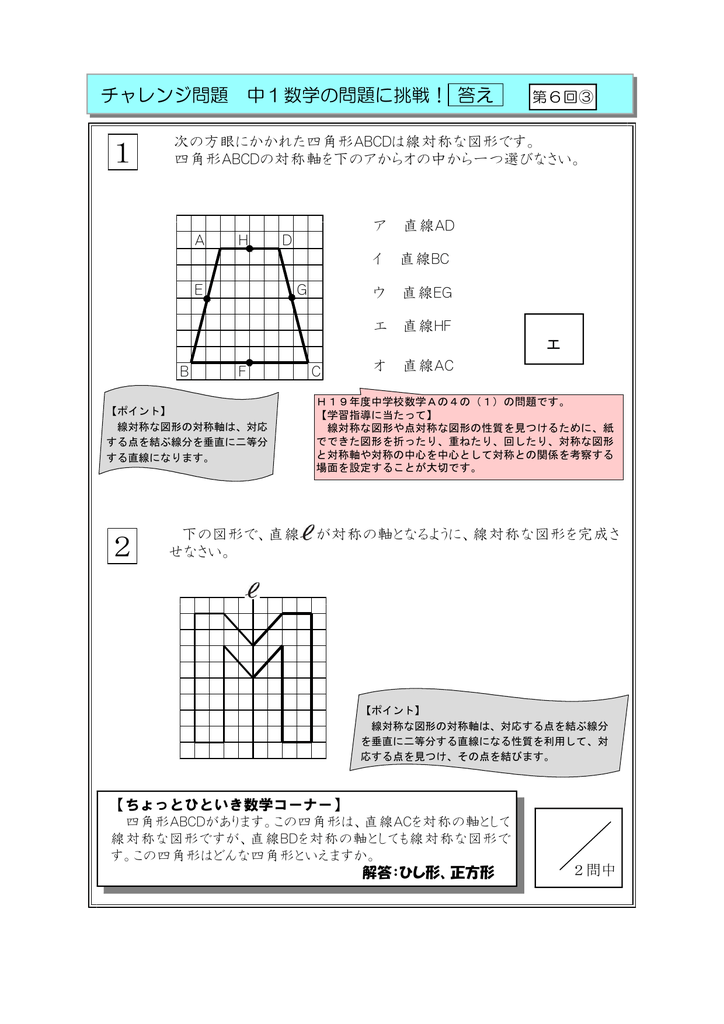
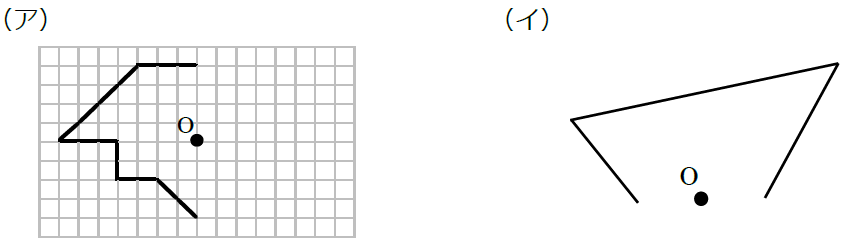
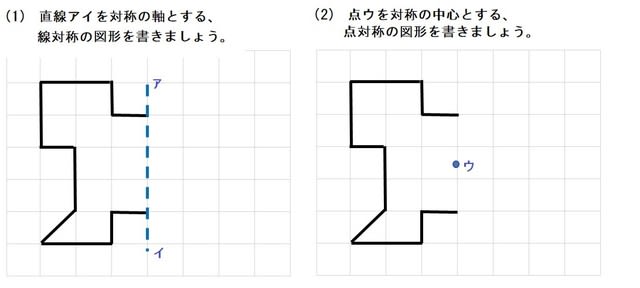
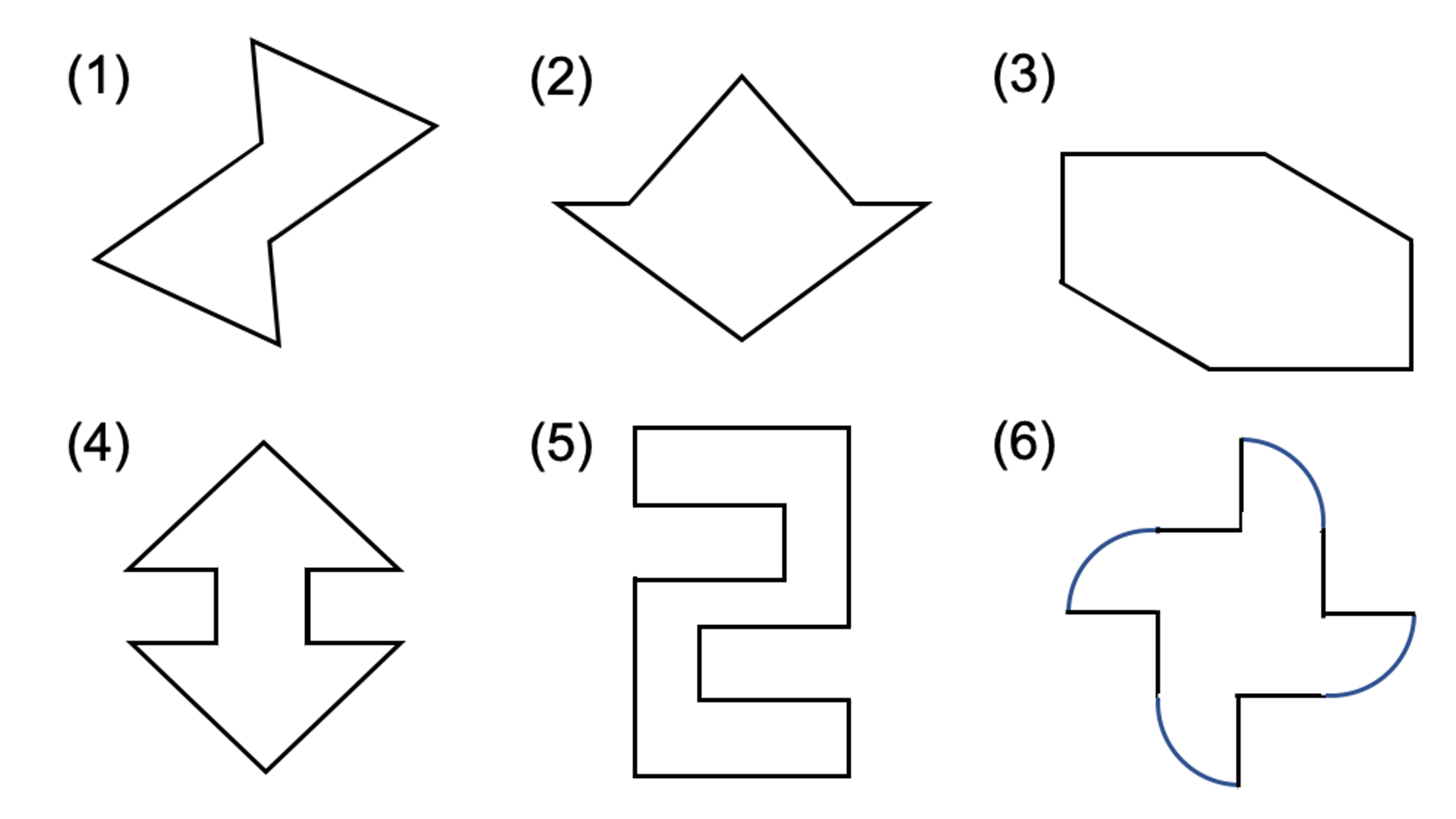
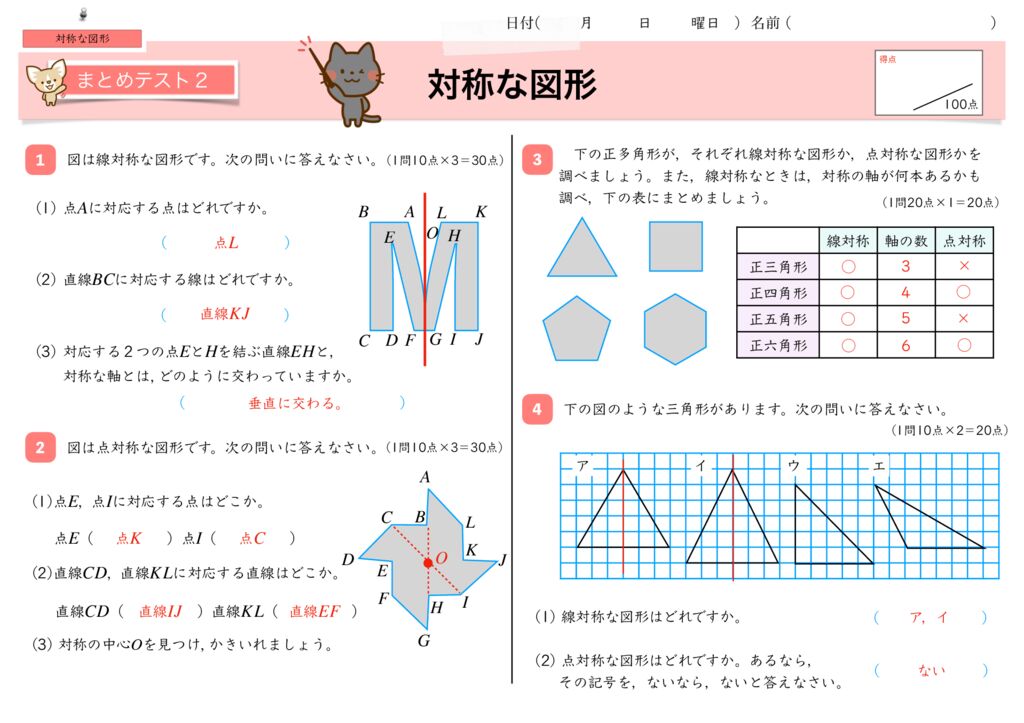
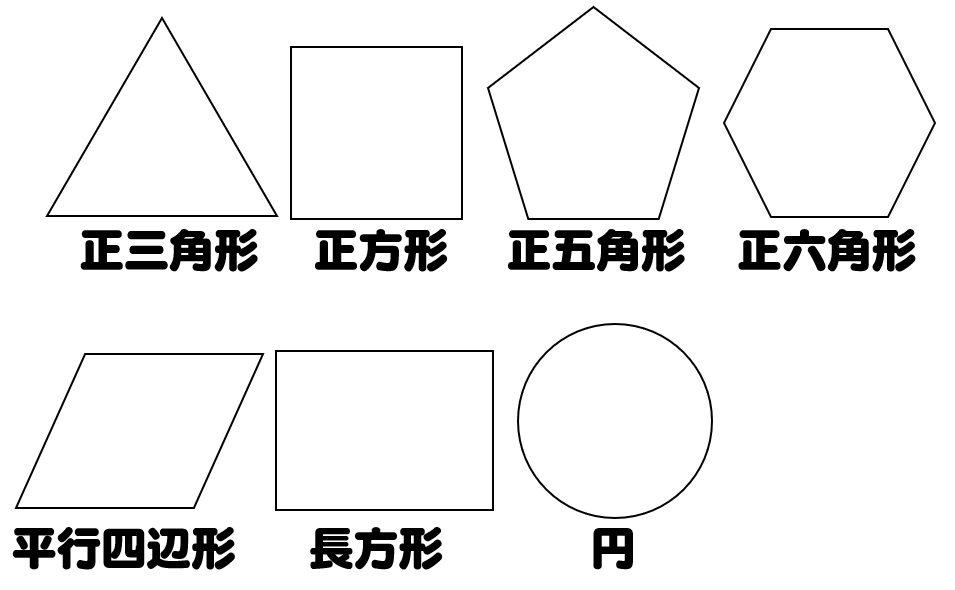
下図は線対称な図形です．対応する辺,角を書きましょう (1) 線対称となる対称軸をかきましょう (2) 角Bに対応する角 (3) 角Cに対応する角 (4) 辺CDに対応する辺 (5) 辺DEに対応する辺 線対称と点対称の図形のドリルです．対称の種類は，線対称と点対称で2択1 次の9個の図形のうち，線対称な図形と点対称な図形はそれぞれ何個ありますか。 2右の図のような正八角形があります。 正方形 直角三角形 二等辺三角形 正三角形 正五角形 正六角形 長方形 平行四辺形 ひし形 ア オ イ ウ エ カ キ ク チャレンジ問題 対称① 直線ABが対称の軸となるような線対称な図形 ② 点Oが対称の中心となるような点対称な図形 4 次の㋐～㋔の図形について，あとの問いに答えましょ う。 ㋐ 平行四辺形 ㋑ 正三角形 ㋒ 正方形 ㋓ 正五角形 ㋔ 正六角形 ① 線対称でも点対称でもある図形は

対称な図形 点対称 問題のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

2	2	2
2	2	2
2	2	2
2	2	2
2	2	2
2	2	2
2	2	2
2	2	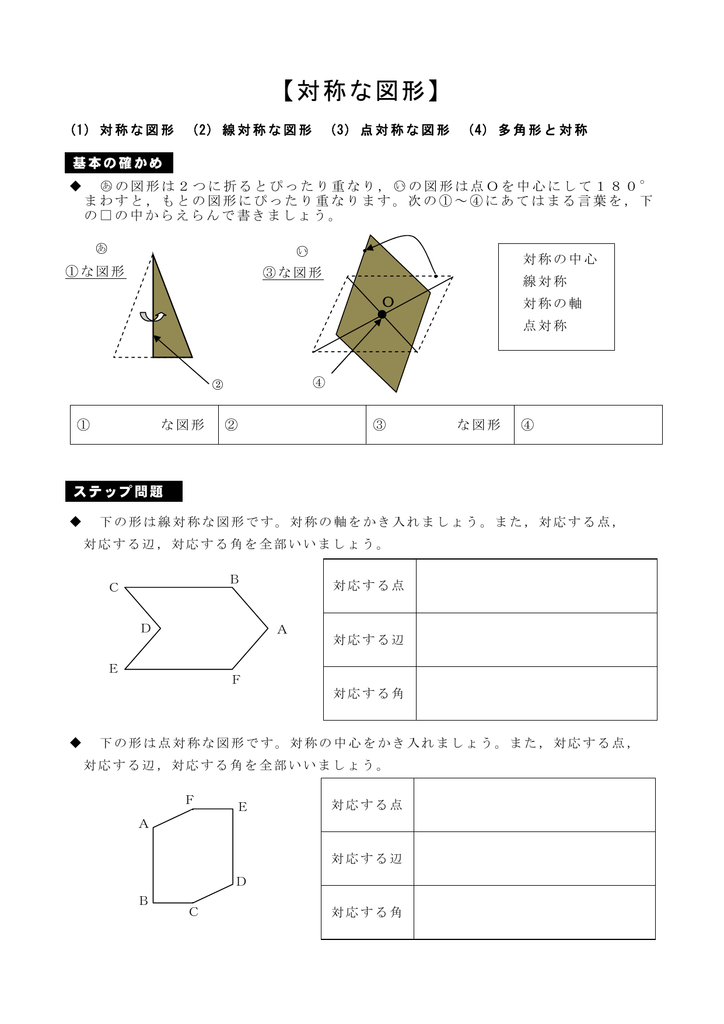2
2	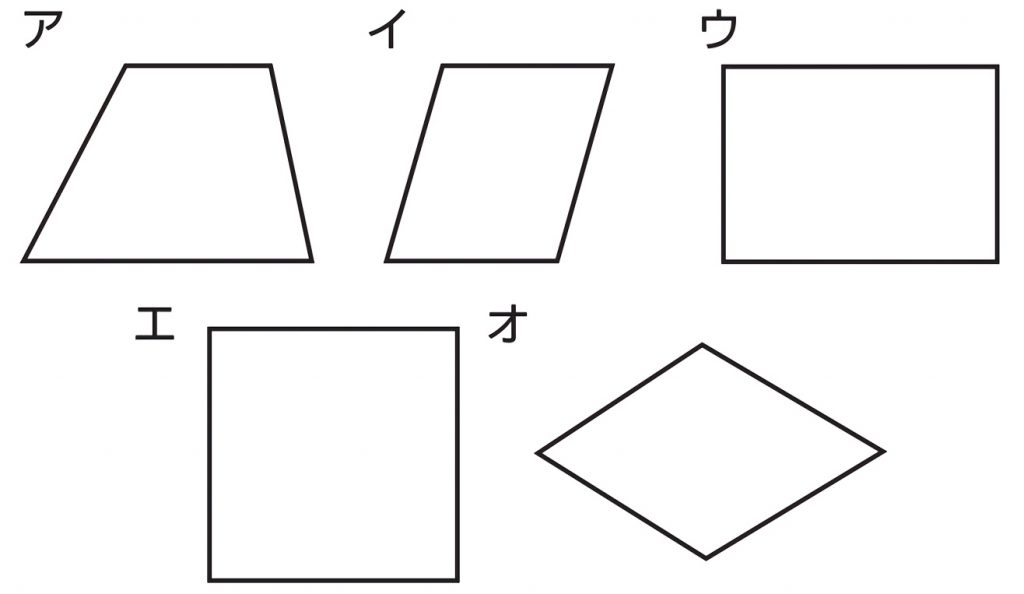2	2
2	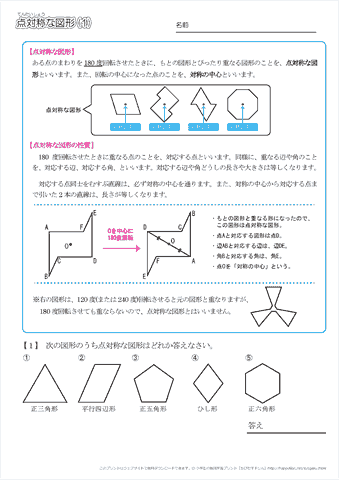2	2
2	2	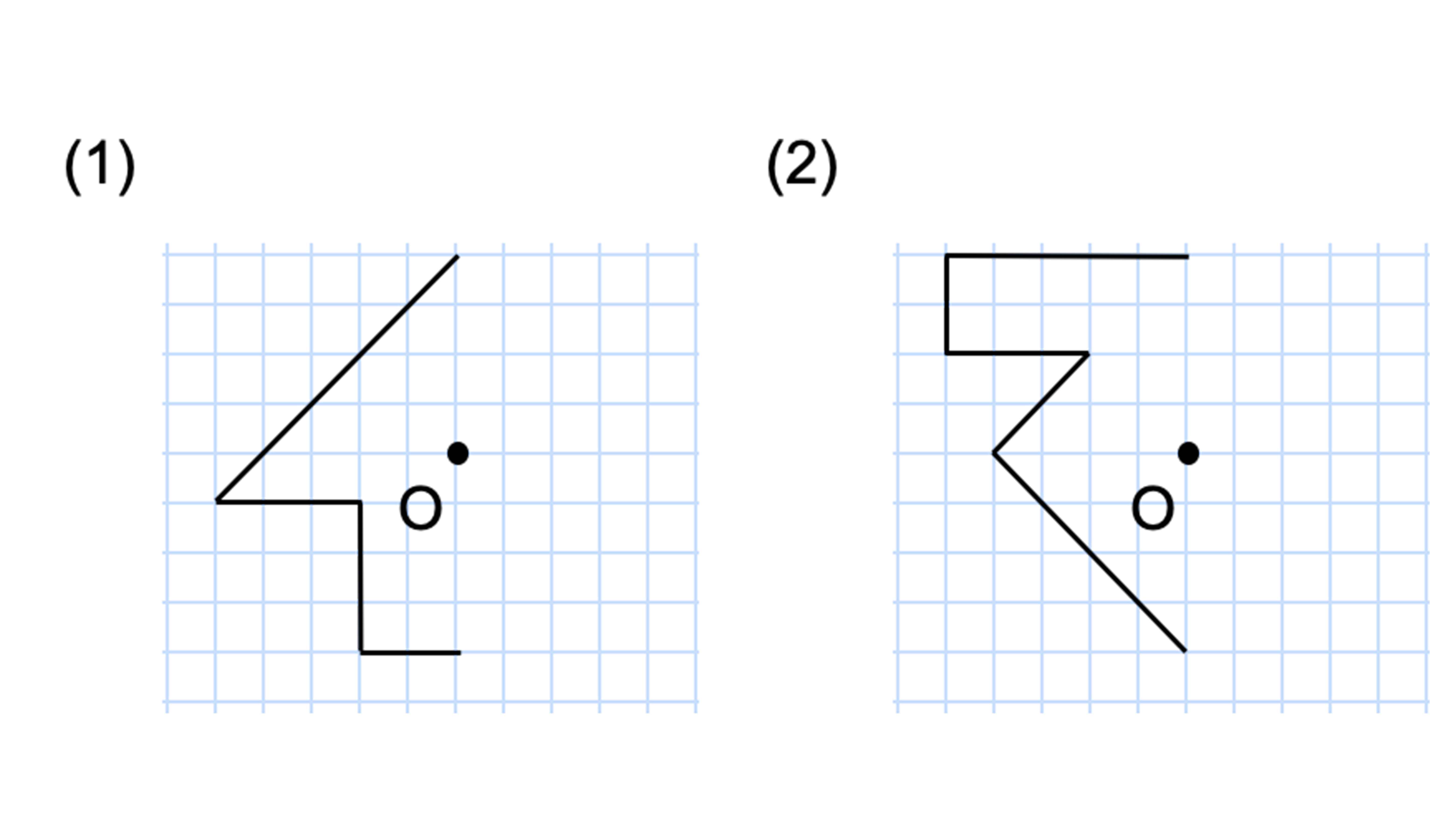2
2	2	2
2	2	2
2	2	2
2	2	2
2	2	2
2	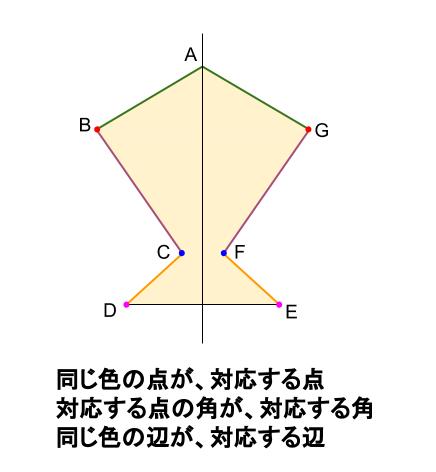2	2
2	2	2
2	2	2
2	2	2
2	2	2
2	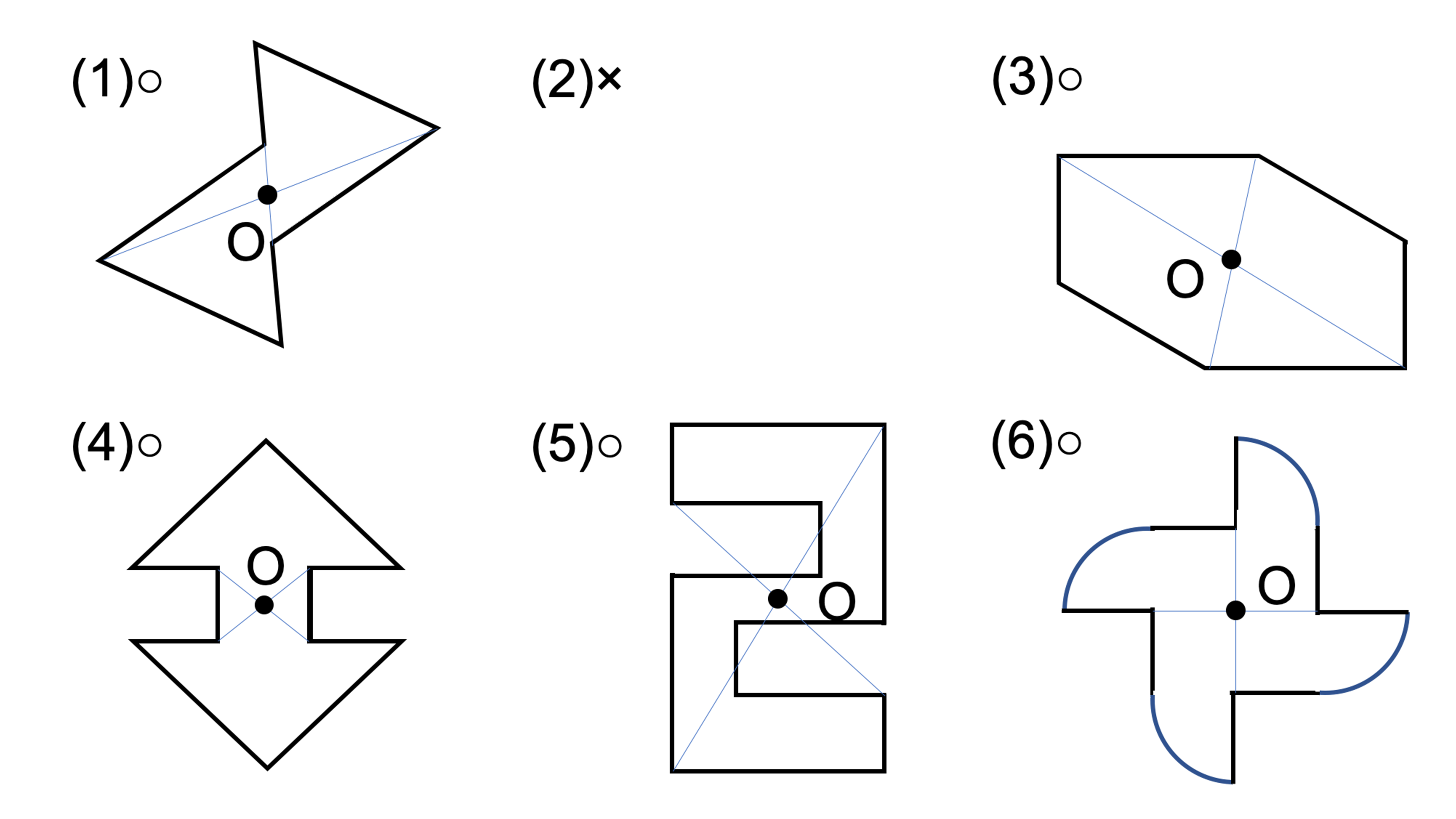2	2
2	2	2
2	2	2
2	2	2
2	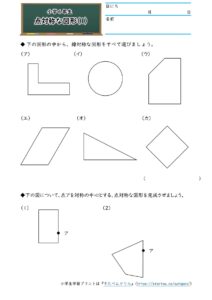2	2
2	2	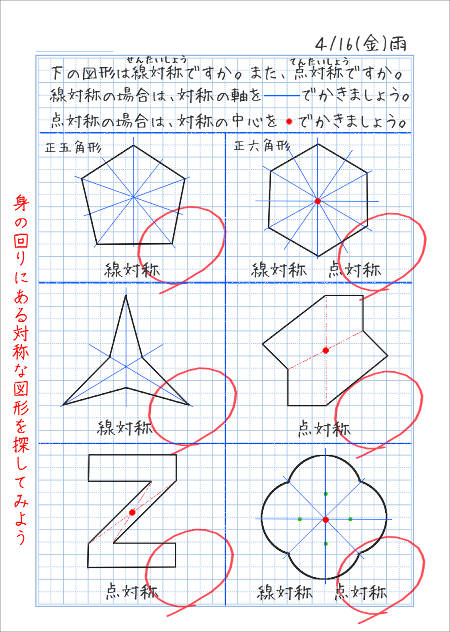2
2	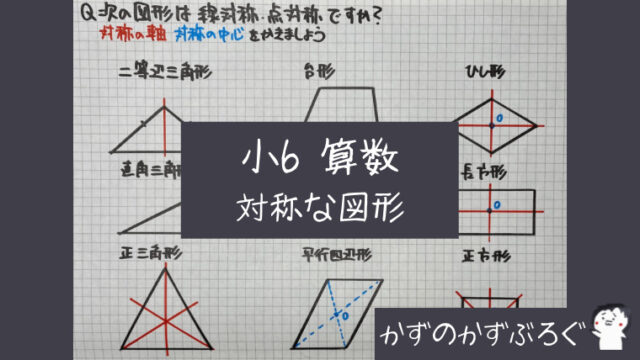2	2
2	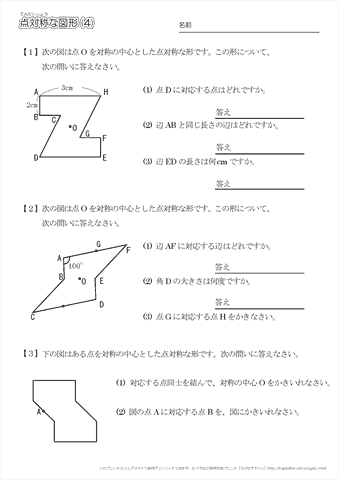2	2
2	2	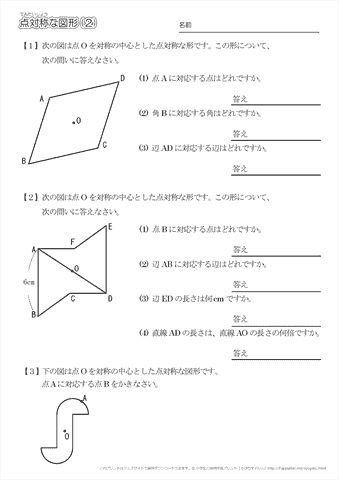2
2	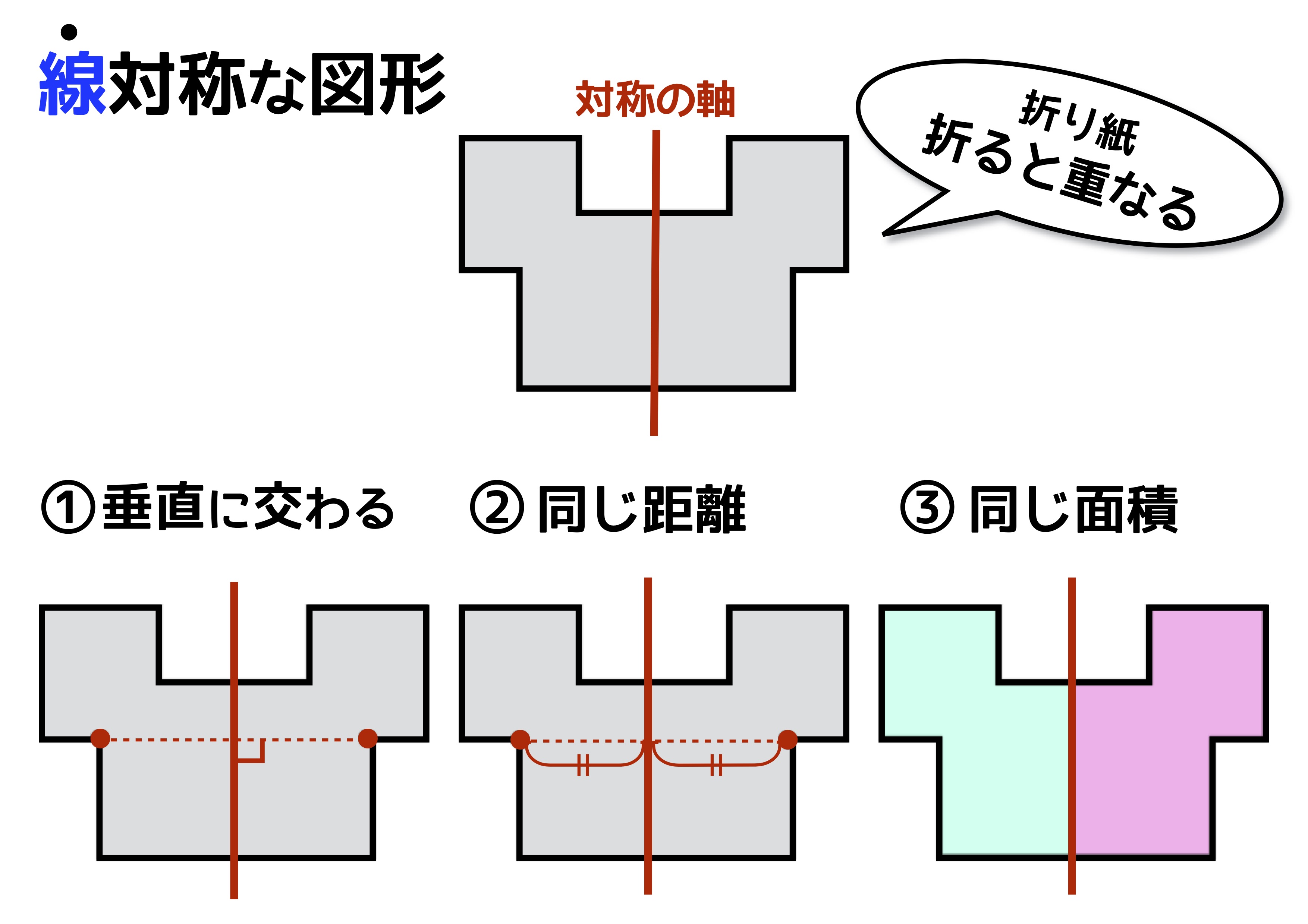2	2
2	2	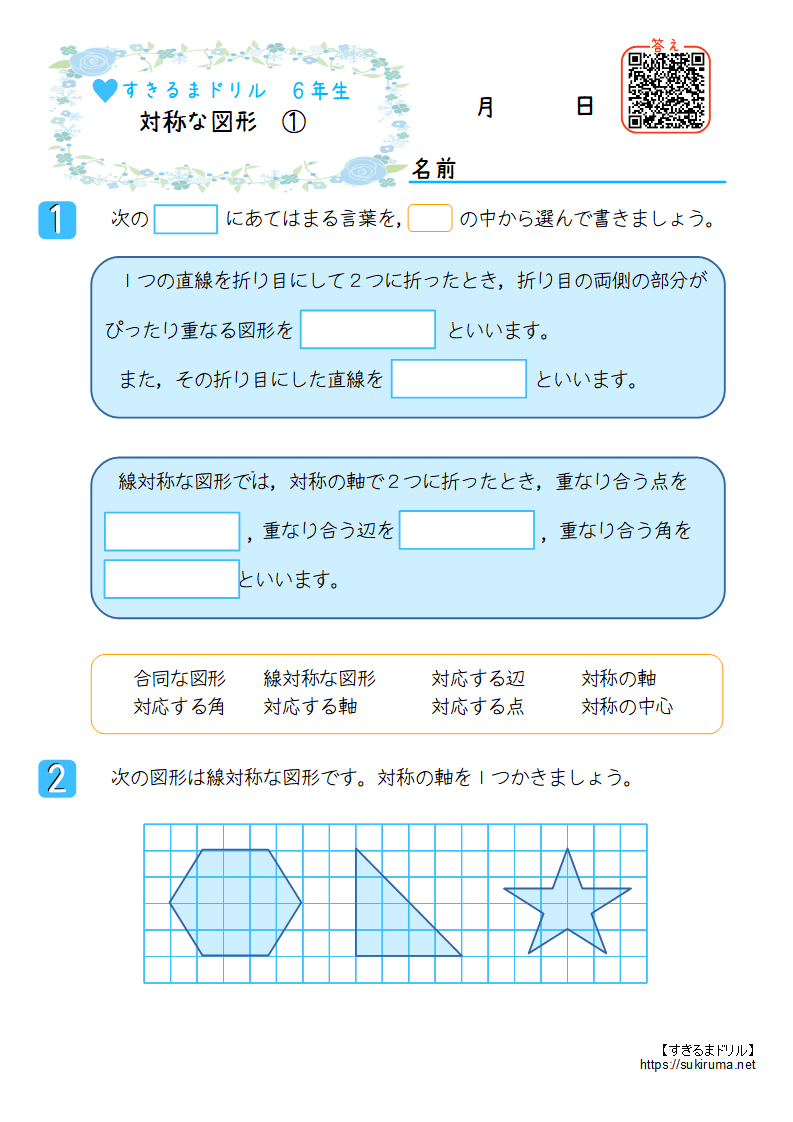2
2	2	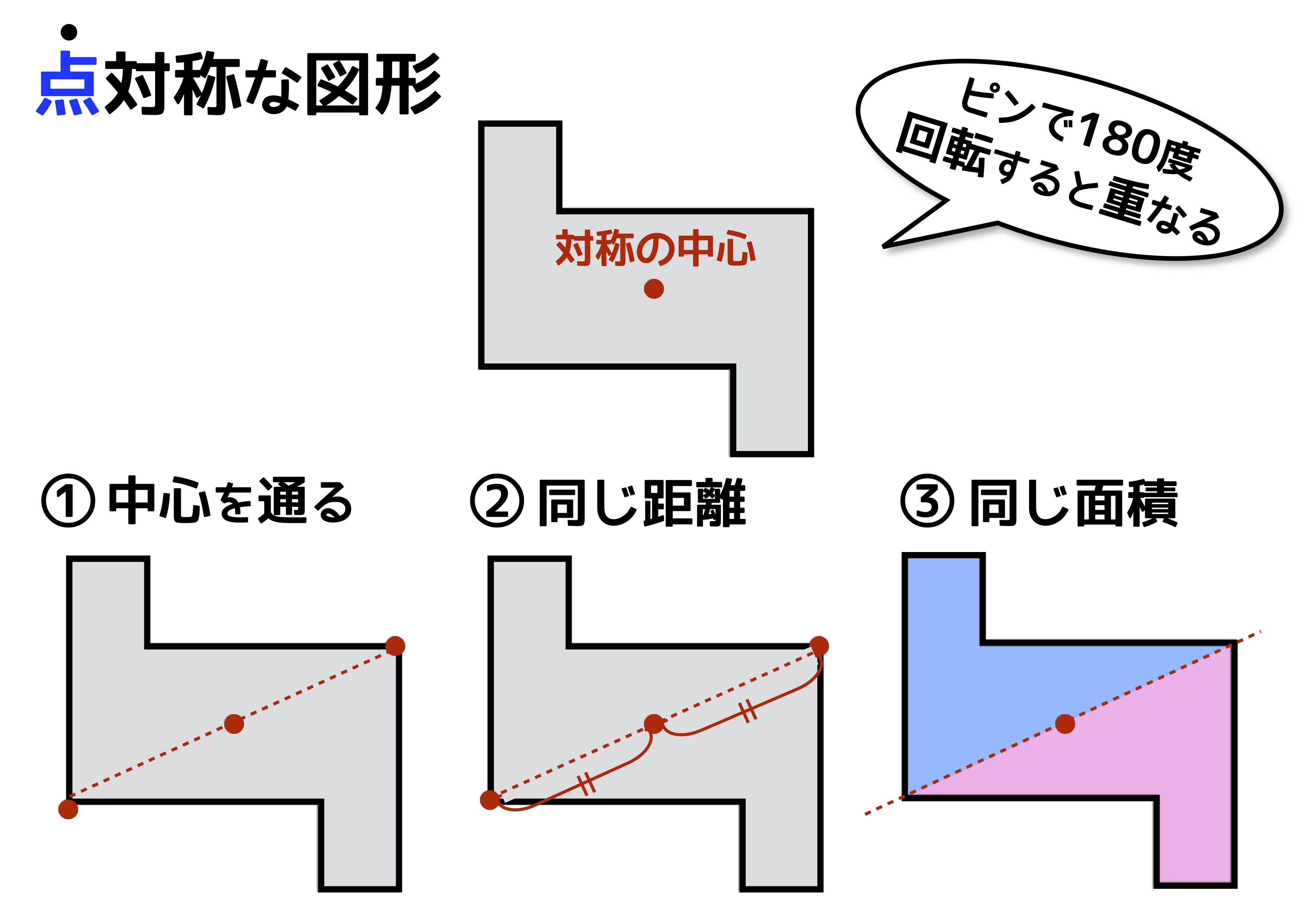2
2	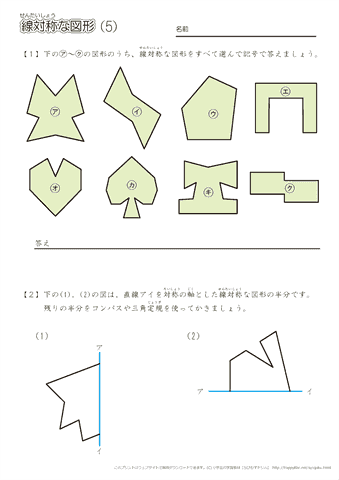2	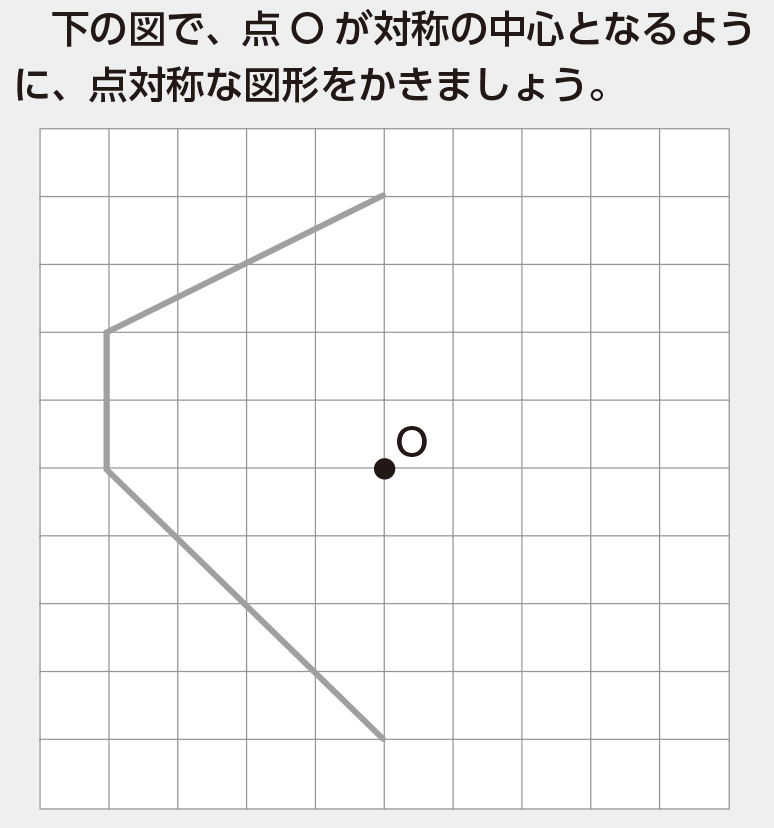2
2	2

 このような問題は今後いくらでも出てくるので、頭の中を時間掛けて良いので自分なりに整理できればと思っています。 6年生最初の単元「対称な図形」 「線対称」「点対称」 ぼくも、忘れていたのか？習っていないのか？小学6年生の算数 線対称な図形 問題プリント 無料ダウンロード・印刷できる、線対称な図形の練習問題プリント です。 線対称な図形の意味と性質、図形さがし、作画などを練習し、理解を確かめることのできるプリントです。

Incoming Term: 対称な図形 問題, 対称な図形 点対称 問題, 算数6年 対称な図形 問題,